/Mathematics/Ê 

PROGRAMSPECIFIK UTBILDNINGSPLANÊ 

c4.1 SyfteÊ 

Genom utbildningsprogrammet för matematik skall den studerande få grundläg gande kunskaper i ämnesområdet matematik samt i programmeringsmetodik för matematiska tillämpningar, fördjupade teoretiska kunskaper inom delar av matematikområdet samt insikt i hur matematiken kan användas inom olika problemområden. €mnesområdet matematik används här som sammanfattande beteckning för delämnena matematik, numerisk analys, optimeringslära och matematisk statistik. Den obligatoriska delen ger en matematisk grund för fortsatta studier även i andra ämnen, såsom ekonomi och biologi.Ê 

Utbildningsprogrammet skall förbereda för yrkesverksamhet med matematisk inriktning i näringslivet och den offentliga sektorn. De teoretiska kunskaperna i matematik skall ha ett sådant djup att den studerande efter studierna har möjlighet att ständigt på nytt anpassa sig till de snabbt växlande kraven i yrkeslivet och också har en grund för att självständigt utveckla ny kunskap inom matematikområdet. Den studerande skall också ha goda förutsättningar att samarbeta med specialister inom andra områden.Ê 

Med val av lämplig inriktning ger programmet även en god bas för fortsatta studier/forskarutbildning inom ämnesområdet matematik.Ê 

c4.2 Programmets uppläggningÊ 

Programmet omfattar maximalt 160 poäng. Det inleds med ett tvåårigt bas block av obligatoriska kurser innehållande 40 poäng i matematik samt vardera 10 poäng i numerisk analys, programmering, optimeringslära och matematisk statistik.Ê 

Basblocket ger grundläggande kunskaper och färdigheter i det matematiska ämnesområdet och är en god grund för fortsatta studier i matematisk-naturveten skapliga ämnen.Ê 

Kurserna läses koncentrerat, normalt ges en kurs i taget. Ett betydande inslag av datorlaborationer finns. Syftet med dessa är dels att ge en uppfattning om olika algoritmers egenskaper genom egna experiment, dels att orientera om existerande programbibliotek och deras användning för att lösa matematiskaÊ 

problem.Ê 

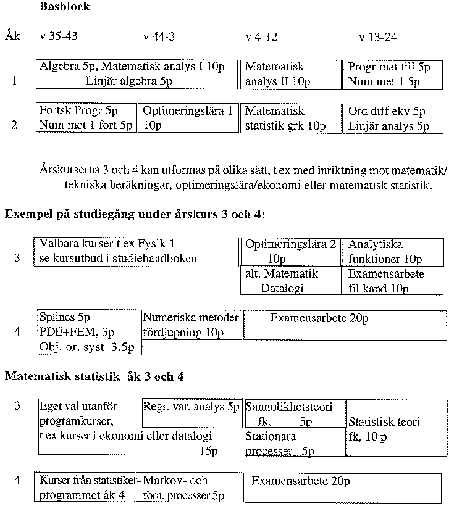
Under tredje och fjärde årets påbyggnadsdel har den studerande stor frihet att kombinera kurser efter eget intresse. En möjlig studiegång visas i block schemat på sid 153. Studier i fysik rekommenderas i första hand till den som är intresserad av att arbeta med tekniska beräkningar.Ê 

I tabellen på sid 154 ges exempel på andra kurser som under läsåret 96/97 kan läsas i mån av plats och förutsatt att den studerande uppfyller förkunskaps kraven. Utbudet av dessa valbara kurser kan variera mellan olika år. Kurserna ger den studerande möjlighet till fördjupning i anslutning till tidigare lästa kurser och möjlighet till mer utpräglad profilering.Ê 

För att möjliggöra ytterligare fördjupning i matematiska ämnen kan även kurser från forskarutbildningen inom matematiska institutionen utnyttjas.Ê 

Utbildningen kan även ges en mera programmeringsinriktad profil. I första hand rekommenderas de datalogikurser som listas i tabellen men det är möjligt att läsa även andra kurser som institutionen för datavetenskap ger inom civilingenjörsutbildning och datavetenskaplig utbildning.Ê 

Matematikprogrammet kan omfatta 160 poäng eller 120 poäng och avslutas med ett examensarbete om 20 resp 10 poäng.Ê 

c4.3 Utbildningens innehållÊ 

Nedan ges en kortfattad presentation av programmets karaktärsämnen. För en utförlig beskrivning av innehållet i olika kurser hänvisas till respektive kurs plan.Ê 

Programmet inleds med att ge de nödvändiga matematiska grunderna. Dessa utnyttjas och befästs sedan i kurserna i numerisk analys, optimeringslära och matematisk statistik.Ê 

Matematiken har länge varit ett hjälpmedel för att beskriva omvärlden. €nda sedan Newton ställde upp reglerna för sin mekanik har matematiken varit det språk som används av vetenskapsmän för att formulera modeller och utveckla teorier inom många områden. I programmet ges kurser i algebra, linjär algebra, matematisk analys, linjär analys och differentialekvationer. Dessutom erbjuds ett flertal andra kurser som ger goda möjligheter till fördjupade eller breddade studier.Ê 

I ämnet numerisk analys utvecklas och analyseras metoder för effektiv och noggrann lösning av naturvetenskapliga och tekniska problem med hjälp avÊ 

datorer. Kurserna Numeriska metoder 1 och Numeriska metoder 1, forts i basblocket presenterar grunderna i ämnet. Påbyggnadskursen Numeriska metoder, fördjupning, ger fördjupade kunskaper om numeriska metoder för problem inom fyra stora områden: lineär algebra, icke-lineär optimering, ordinära och partiella differentialekvationer. Användning av splinefunktioner för datorstödd konstruktion behandlas i en separat kurs.Ê 

För att kunna använda datorer som hjälpmedel för att lösa matematiska problem, krävs även kännedom om datorer och färdighet att använda programmeringsspråk. Detta förmedlas i grundkursen i programmering. I fortsättningskursen fördjupas dessa kunskaper. €ven teknik för icke-nume riska tillämpningar behandlas i denna kurs.Ê 

Inom ämnet optimeringslära studeras optimeringsmodeller och tillhörande metoder för analys av olika typer av beslutsproblem inom områdena teknik, ekonomi och samhälle. Det matematiska verktyget är matematisk programme ring som inkluderar bl a lineär programmering, icke-lineär programmering och heltalsprogrammering. I matematikprogrammet ges en grundkurs i optimerings lära och en påbyggnadskurs.Ê 

€mnet matematisk statistik behandlar modeller för försök, vilkas resultat påverkas av slumpmässiga faktorer. I sannolikhetsläran arbetar man med konstruktion och analys av slumpmodeller med vilkas hjälp sannolikheter för intressanta händelser kan beräknas och variationer i mätvärden förklaras. Statistisk teori innehåller metoder för att utgående från observerade data dra slutsatser om de system som genererat data samt bedöma osäkerheten i slutsatserna. Statistiska metoder har tillämpningar inom medicin, teknik, naturvetenskap, ekonomi, etc. I matematikprogrammet ges en grundkurs i matematisk statistik inom det obligatoriska blocket samt flera fortsättningskur ser.Ê 

c9.4 Tröskelregler för uppflyttande till årskurs treÊ 

För att en programstuderande skall få påbörja kurser inom matematikområdet i programmets tredje och fjärde år fordras att kursernas förkunskapskrav är uppfyllda.Ê 

En studerande som inte uppfyller kraven för att få börja i årskurs tre skall i samråd med studievägledare lägga upp ett individuellt studieprogram.Ê 

c4.5 ExamensarbeteÊ 

Med examensarbetet, som avslutar utbildningen, skall den studerande visa sin förmåga att tillämpa under studietiden förvärvade kunskaper genom att själv ständigt behandla en förelagd uppgift och redovisa sina kunskaper och resultat muntligt och skriftligt. För godkänt examensarbete på D-nivå krävs det också att den studerande genom opposition vid framläggning av annat examensarbete visat sin förmåga att kritiskt granska och diskutera en i tal och skrift presenterad teknisk eller vetenskaplig rapport.Ê 

Uppgiften för examensarbetet hämtas ofta från ett företag eller en myndighet, men kan även härröra från ett forskningsprojekt inom matematiska institutio nen. Medan handledaren i regel är knuten till det ställe där examensarbetet utförs, skall examinator, dvs den som bedömer arbetet, tjänstgöra som lärare vid matematiska institutionen. Val av examinator görs med tanke på examens arbetets inriktning. Den studerande skall kontakta en examinator, visa en skriftlig arbetsplan för aktuellt projekt, redovisa uppfyllda förkunskapskrav och få klartecken från examinatorn innan ett examensarbete påbörjas.Ê 

För att få magister- (kandidat-) examen i matematik skall examensarbetet utföras med anknytning till något av ämnena matematik, numerisk analys, matematisk statistik, optimeringslära.Ê 

För närmare information om opposition, examensarbetets utförande och rapport ens omfattning och utformning hänvisas till särskilda anvisningar från mate matiska institutionen.Ê 

För att få påbörja ett examensarbete om 10p på C-nivå för filosofie kandidatexa men skall den studerande ha godkänts i kurser om minst 80 poäng, varav minst 60 poäng skall ligga inom huvudämnet matematik. Speciellt skall följande kurser, eller motsvarande, vara godkända:Ê 

·Algebra, 5p (NMAA11)Ê 

· Linjär algebra, 5p (NMAA12)Ê 

· Matematisk analys 1 och 2, 20p (NMAA13 och NMAB13)Ê 

samt alternativtÊ 

· Linjär analys, 5p (NMAC07) och Ordinära differentialekvationer, 5pÊ 

(NMAC08)Ê 

ellerÊ 

· Analytiska funktioner, 10 p (NMAC09)Ê 

För att få påbörja det avslutande examensarbetet om 20 poäng för magister examen skall den studerande ha godkänts i kurser om minst 120 poäng, varav minst 80 poäng skall ligga inom huvudämnet matematik. Speciellt skall följande kurser, eller motsvarande, vara godkända:Ê 

· Algebra, 5p (NMAA11)Ê 

· Linjär algebra, 5p (NMAA12)Ê 

· Matematisk analys 1 och 2, 20p (NMAA13 och NMAB13)Ê 

· Linjär analys, 5p (NMAC07)Ê 

· Ordinära differentialekvationer, 5p (NMAC08)Ê 

· Analytiska funktioner, 10p (NMAC09)Ê 

För att få påbörja ett examensarbete om 10 poäng på D-nivå som komplettering av tidigare examensarbete om 10 poäng på C-nivå, skall den studerande uppfylla samma tröskelregler som för examensarbetet om 20 poäng för magisterexamen och dessutom ha fullgjort ett godkänt examensarbete om 10 poäng.Ê 

Fördjupade studier utöver villkoren ovan kan krävas beroende på examens arbetets inriktning.Ê 

Reglerna om tid för påbörjande av examensarbete gäller också för opposition av examensarbete.Ê 

c4.6 ExamensförordningÊ 

Programmet avslutas med filosofie magisterexamen eller filosofie kandidatexa men med matematik som huvudämne.Ê 

Examina regleras av högskoleförordningen, se allmänt avsnitt i handboken.Ê 

c4.7 Särskild behörighetÊ 

För att antas till matematikprogrammet krävs, förutom villkoren för grundläg gande behörighet, följande standardbehörighet:Ê 

Standardbehörighet E.2.1:Ê 

Matematik E, Fysik B och Kemi A.Ê 

c4.8 Blockschema för matematikprogrammetÊ 

UTBILDNINGSPROGRAM FÖR MATEMATIKÊ 

Ê 

Ê